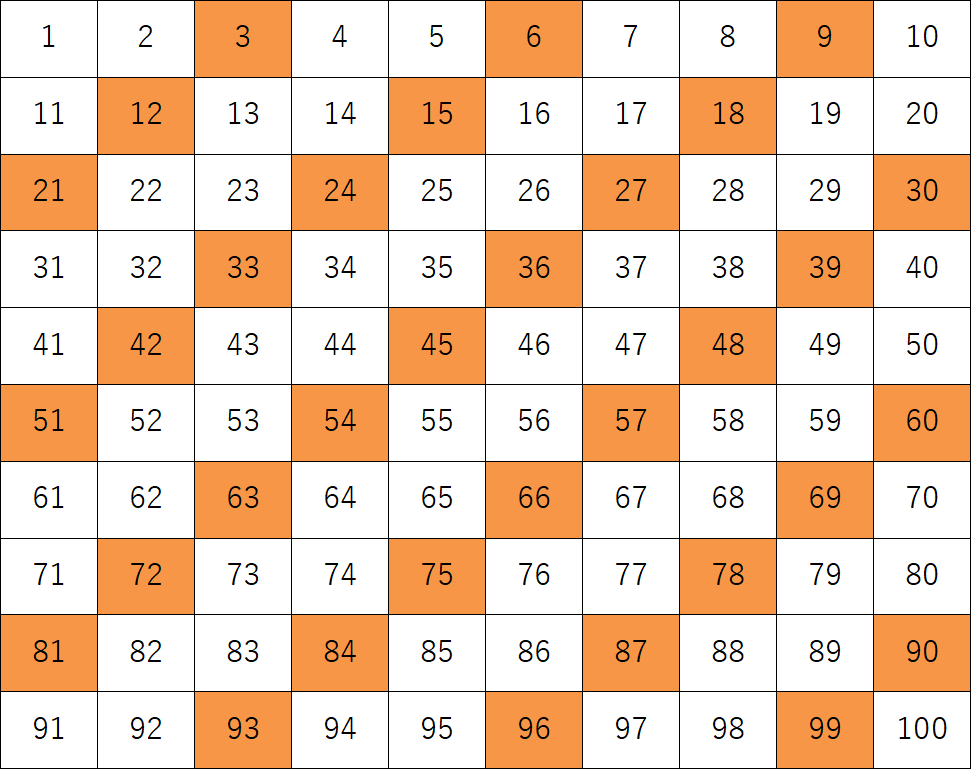
3の倍数の性質と見分け方（3の倍数早見表つき）

ある整数が 3 の倍数であるかどうかは「その数の各位の数を足した値」が 3 の倍数であるかどうかで調べられます．

例えば 123 は各位の数を足すと $1 + 2 + 3 = 6$ となり，6 は 3 の倍数．したがって 123 は 3 の倍数となります．

今度は 75912 を考えてみましょう．各位の数を足すと $7+5+9+1+2=24$ となり，24 は 3 の倍数です．したがって 75912 は 3 の倍数となります．

問題

次の数が 3 の倍数であるか確かめなさい．

1. 111
2. 765
3. 392
4. 5827
5. 6195

解答

1. 1+1+1=3 となり，3 は 3 の倍数であるから 111 は 3 の倍数
2. 7+6+5=18 となり，18 は 3 の倍数であるから 765 は 3 の倍数
3. 3+9+2=14 となり，14 は 3 の倍数でないから 392 は 3 の倍数でない
4. 5+8+2+7=22 となり，22 は 3 の倍数でないから 5827 は 3 の倍数でない
5. 6+1+9+5=21 となり，21 は 3 の倍数であるから 6195 は 3 の倍数

追記

上の問題から 3 桁の 3 の倍数について重要な性質がわかります．

1. 111 のように各位の数が同じ 3 桁の整数は 3 の倍数
2. 765 のように各位が連続している 3 桁の整数は 3 の倍数

1 の例としては

111
222
333
444
555
666
777
888
999

があります．各位の数が同じであるため，各位の数を足すと必ず 3 の倍数となります．

2 の例としては

123
234
345
456
567
678
789
987
876
765
654
543
432
321

があります．各位が連続していると，各位の合計値は中央の数を 3 倍した値になるためです．ではなぜ各位の数の合計値が 3 の倍数であると，その数自体も 3 の倍数となってしまうのでしょうか？

証明

まず 2 桁の数から考えてみます．

2 桁の数を $a×10+b$ と表します．ここで a は十の位，b は一の位です．例えば 34 は $3×10+4$ となります．

各位の合計は $a+b$ ですが，これが 3 の倍数であるとしましょう．すると $a+b=3m$ （mは整数）となります．すると

a×10+b
=a×9+a+b
=a×9+3m
=3(3a+m)

となり $a×10+b$ が 3 の倍数であるとわかります．3 桁の数も 4 桁の数も同様に証明できます．

3の倍数早見表